XII. Nature’s Numbers and Counting System
[Contd. A Journey to the Wonderland of Math. by Ajay Kumar Chaudhuri]
Marvellous beauty of Nature is an aesthetic marvel of numbers.
[Contd. A Journey to the Wonderland of Math. by Ajay Kumar Chaudhuri]
Marvellous beauty of Nature is an aesthetic marvel of numbers.
Have you ever noticed how the plants grow their branches over a considerable period of time after germination from seeds? Or have you think of the number of petals and their arrangements in flower of plants,those blossom everyday here and there in front of our eyes? Likewise ,do you know the numbers of seeds a multi seed plant pack in their fruits and their arrangements inside it?
If you observe
carefully, you will find in each of the above cases an astonishing pattern in
which numbers play a very important role in an orderly manner. We will explore
those mysteries shortly.
In fact, these
rules of numbers are found in innumerable things of nature around us.
Look at the amazing structure of
shells of different snails, such as Chambered Nautilus or observe the body of
the star fish which has 5 arms with beautiful five-point symmetry. Inside the
fruits of many plants we also find this rule of numbers : the banana has 3
sections while an apple has 5, for example.
Have you ever
thought of the number of bones in your fingers? You know that you have 8
fingers in total, 5 digits on each hand, 3 bones in each finger, 2 bones in a
thumb and one thumb in each hand.
So, if we arrange
these numbers in an ascending order, it will be
1,
1, 2, 3,
5, 8
That means
1, 1, 1+1,
1+2, 2+3, 3+5
Is it not striking? For, each number beginning from the
third, is the sum of the previous two numbers. Following this rule, if we
extend this array, we get
1, 1, 2, 3, 5, 8, 13, 21, 34, 55,
89, 144 ----- to as far as we please.
This type of
array of numbers obeying definite rule or rules is called a “Sequence” or
“Series” in mathematical term. We shall see shortly the great importance and
amazing role of these numbers in nature – in plants, leaves, flowers, seeds,
creatures big or small, in our very human body, in art, music, sculpture,
architecture such as in the great Egyptian pyramids and many other famous
ancient monuments.
Often, especially
in modern usage, this sequence is extended by one more initial term :
0, 1, 1, 2, 3, 5, 13, 21, 34 ----
This sequence is
named after its inventor, a famous Italian mathematician Leonardo of Pisa,
better known as Fibonacci*, The “Fibonacci Sequence” and each number comprising
the sequence is also called “Fibonacci numbers” or may be called nature’s
numbers for their wide spread presence in nature.
[* Leonardo Fibonacci (1170 – 1250
AD)
(Pronounced as : fib – on – arch – ee or fee
– bur – narch – ee)
Fibonacci was an Italian mathematician, considered to be the most
talented mathematician of the Middle Ages. Not much is known about the life of
Fibonacci.
He was born around 1170 in Pisa in a wealthy merchant family. As a young
boy, he travelled with his father to North-Africa on a business trip of his
father and it was in Bugia, now Algeria that he learned about Hindu-Arabic
numeral system.
Fibonacci travelled extensively around Mediterranean Coast, meeting many
merchants and learning about their systems of doing arithmetic. He soon
realized the many advantages of the Hindu-Arabic system. In 1202 he completed
his famous book “Liber Abaci” essentially a book of calculations which
popularized Hindu-Arabic numerals in Europe.
The date of Fibonacci’s death is not known, but has been estimated to be
around 1240 and 1250, most likely in Pisa.]
One thing is to
be remembered that Fibonacci was not the first to know about the sequence, it
was known in India hundreds of years before!
The so called
Fibonacci sequence appears in Indian mathematics in connection with Sanskrit
Prosody. There are clear evidences of applications of Fibonacci numbers in the
writings of Pingala (200 BC), Virhanka (700 AD) and Hemchandra (1150 AD). Outside
India, Fibonacci sequence first appeared in Liber Abaci by Fibonacci.
A closer
inspection of the numbers making up Fibonacci Sequence brings light a good
number of fascinating patterns and mathematical properties.
The most
important and interesting of them is the idea of “Golden Ratio”. The very name
suggests that it is the name of a ratio. In fact, it is called by many other
names, such as “Golden Mean”, “Golden Section”, “Divine Proportion” and also a
“Golden Number”. So, it is amply clear that this ratio is not an ordinary one
but of great fame and importance. Now it is popularly known by the upper case
Greek letter Փ
, phi.
This Golden Ratio
has been claimed to have held a special fascination for at least 2400 years,
though without proof. Some of the greatest mathematical minds of all ages, from
Pythagoras and Euclid in ancient Greece, through the medieval Italian
mathematician Leonardo of Pisa, Fibonacci and the Renaissance astronomer Johannes
Kepler, to present day scientific figures such as Oxford physicist Roger
Penrose, have spent endless hours over
this simple ratio and its properties. But the fascination with the Golden Ratio
is not confined just to mathematics. Biologists, artists, musicians,
historians, architects, psychologists and even mystics have pondered and
debated the basis of its ubiquity and appeal. In fact it probably fair to say
that Golden Ratio has inspire thinkers of all discipline like no other number
in the history of mathematics.
I think, now you
are very much curious to know what this extraordinary ratio is!
If we go further
and further and take ratios of two Fibonacci numbers, obeying the above rule,
we will get more and more accurate values of the golden ratio but never arrive
at exact value.
We have already
calculated the approximate value of the golden ratio as 1.618033988. So it has
two parts – the integral part I and the decimal or fractional part
0.6180339887. One interesting thing is that the nature itself has adopted this
fractional part for the spirals in seed heads and arrangement of leaves in many
plants. So, considering its importance, it is separately denoted by the
lowercase Greek letterφ. In fact Φ
and φ play
amazing role in nature and in many aspects of our lives.
This symbol phi
for the golden ratio was first introduced by an American mathematician Mark
Barr in 1900’s. It has some interesting aspects as well as inner meaning. The character
for phi also has some interesting theological implications.
The description of
this proportion as Golden and Divine is fitting because it is seen by many to
open the door to a deeper understanding of beauty and spirituality in life.
That’s an incredible role for a single number to play but again this one number
has played an incredible role in human history and the universe at large.
The meaning
hidden in phi from the theological aspect is as :
The message from
scripture of all the major monotheistic religions such as in the belief of the
religions Judaism, Christianity and Islam that God is one and only one, he who
created the universe from nothing, splitting, nothingness to offsetting
energies and elements. This view has been substantiated by our modern science.
Today we understand the universe to consist of positive and negative atomic and
subatomic particles and charges, matter and anti-matter, all coming from a
singularity in what we term the “Big Bang”.
The essence of
the Big Bang theory is that, this universe was originated from the explosion of
a very very minute particle, like a grain of sand, under unimaginably high
gravitational pressure. There was nothing, what so ever, of today’s universe.
So it may be conjectured that the baby universe was born from nothing or
started life from zero.
The Fibonacci
numbers may be called the Nature’s numbering system. For, they appear everywhere
in Nature, from the leaf arrangements in plants, to the pattern of florets of a
flower, the bracts of pinecone, the scales of a pineapple, in vegetables and
fruits, seed heads, animal bodies including our human bodies. The Fibonacci
numbers are therefore applicable to the growth of every living thing, including
a single cell, a grain of wheat, a hive of bees and even all mankind.
Without knowing
this sequence plants grow in the most efficient ways. Many plants show the
Fibonacci numbers in arrangements of the leaves around the stem. Many flowers
like daisies, sunflower, rose also show these numbers. Many other plants with
more than normally thickened and fleshy leaves, like Aloe Vera, fall in the
category of “Succulents” manifest these numbers. Some plants having needle-
shaped or scale-leaved, fall in the class of “Coniferous”, also show these
numbers in the bumps on their trunks. Palm trees show the number in the rings
on their trunks.
But the question
is : why do these arrangements in mathematical order occur? In the case of leaf
arrangements in some plants, one of the causes may be related to the maximizing
the space for each leaf or average amount of light falling on each one. In case
of close packed leaves in cabbages and succulents, the correct arrangement may
be crucial for availability of space.
If we look
closely the natural world around us, we can find many instances of mathematical
order involving Fibonacci numbers themselves and closely related Golden
elements.
Many plants
during their growth show Fibonacci numbers in its growing points. Suppose, when
a plant puts out a new shoot has to grow two months before it is strong enough
to support branching. If it branches every month after that at the growing
points we get the picture as shown below [
Pic. No.4 : Fibonacci numbers in growth of plants]
Pic. No.4 : Fibonacci numbers in growth of
plants
Also many plants
show Fibonacci numbers in the arrangements of the leaves around their stems. In
an estimate, it is revealed that 90 percent of all plants exhibit this pattern
of leaves involving these numbers.
It we look down
on a plant we will find, the leaves are often arranged so that leaves above do
not hide leaves below. The reason is obvious that each gets a good share of the
sunlight and catches the most rain to channel down to the roots as it runs down
the leaf to the stem.
Botanists have
noticed spiral growth of plants in many aspects such as in the arrangement of
leaves, florets, seeds of flowers and fruits and other structures. It is also
revealed by close observations that plants grow new cells in spirals. This
spiral happens naturally because each new cell is formed after a turn. The
seeds of a sunflower, the spines of a cactus and bracts of a pinecone all grow
in whirling spirals patterns. Remarkable for their complexity and beauty, they
also show consistent mathematical patterns that scientists have been striving
to understand. A large number of plants have spiral patterns in which each
leaf, seed or other structures follow the next at a particular angle, called
the “golden angle” which is about 137.50. This golden angle is
closely related to the golden ratio which ancient Greeks studied extensively
and some had believed to have divine, aesthetic or mystical properties.
Scientists have
puzzled over this pattern of plant growth for hundreds of years. Why do plants
prefer the golden angle to any other? And how can plants possibly “know” anything
about Fibonacci numbers?
Early researchers
thought these patterns provide an evolution advantage and survival for plants.
But most recently they have realized that the answer lies in biochemistry of
plants as they develop new leaves, flowers or other structures. The mystery has
not been solved entirely but a basic understanding of the process seems to be
in sight. For searching these answers, botanists have gone back to their
electron microscope to re-examine plants they thought that they had already
understood.
The arrangements
of leaves in plants obey mathematical diktat such as Fibonacci sequence, golden
angle, golden ratio etc. The pattern of arrangements of leaves on the stem is
called “Phyllotaxy”. As a stem grow at its apex new leaf buds form along the
stem by a highly controlled development process. Leaf arrangement along the
plant stem depends on the species and is an important identifying
characteristic.
If we look around
the beautiful botanic garden of nature we will find the basic phyllotactic
patterns in the plant kingdom are either opposite, whorled or alternate.
When two leaves
arise at each node opposite to each other the phyllotaxy is “opposite”. When
each pair at each node placed at right angles to one another it is termed as
“opposite decussate” such as in latex producing plants, guava etc. But if all
the pairs occur in same line, the phyllotaxy is “opposite superposed” Jamun is
an example.
If more than two
leaves arise at a each node in the shape of whorl, it is called “whorled”,
phyllotaxy as in oleander.
More than 80% of
the 250,000 higher plant species have an “alternate” phyllotaxis, as in the case
of potato, araucaria, yucca or sunflower for instances. Alternate phyllotaxis
again manifests in two classes – “spiral” and “multijugate”.
In the natural
process, leaves grow in the plants from their leaf primodia, the embryo of
leaves, at the nodes of the plants.
In spiral
phyllotaxis, leaf primodia grow on per node, each at a constant divergence
angle of 137.5 degrees from the previous node.
Very often
multijugate patterns look very similar to spiral patterns. The only way to
detect them is to count number of spirals, called the parastiches, visible in
the pattern. If the parastiches numbers do not have a common divisor other than
1, the pattern is spiral phyllotaxy. If these numbers, on the other hand, have
a common divisor, say K, the pattern is called multijugate or more precisely K
– Jugate and there are K elements or leaves at each node.
Fibonacci numbers
occur when counting both the number of times we go around the stem, going from
leaf to leaf, as well as counting the leaves we meet until we encounter a leaf
directly above the starting one. If we count in other direction, we get a
different number of turns for the same number of leaves. We will be surprised
to know that the number of turns in each direction and the number of leaves met
are three consecutive Fibonacci numbers!
If we have 3
clockwise rotations before we meet a leaf directly above the first passing 5
leaves where as if we go anti-clockwise, we need only two turns, than it is
written as 3/5 or 2/5
respectively.
The sunflower
here when viewed from the top shows the same pattern. Starting at the leaf
marked x, we find the next lower leaf turning clockwise. [Pic. No.5 : Leaf arrangements in Sunflower plants] Numbering the
leaves produces the patterns shown here in the picture.
We see that the
third leaf and the fifth leaves are nearest below our starting leaf but the
next nearest below is the eighth then the thirteenth. If we make a list of how
many turns did it take to each leaf will be as
Leaf
number
|
Turns
clockwise
|
3
|
1
|
5
|
2
|
8
|
3
|
All the numbers in each column are Fibonacci numbers!
We find Fibonacci
leaf arrangement in many common trees, such as 1/2 in elm, linden, lime,
grasses 1/3 in beech, hazel, grasses, blackberry 2/5 in oak, cherry, apple,
holly, plum 3/8 in poplar, rose, pear, willow 5/13 in pussy, willow, almond. [Pic. No. 6 : Spiral leaf arrangements]
Pic. No.6
Perhaps there is
none of us who but loves flowers. Everyone has more or less, attractions to
flowers for their exotic beauties, eye-soothing colours of wonderful variety of
shades and sometimes for their mind-boggling fragrances.
But probably most
of us have never taken the time to examine very carefully the number or
arrangement of petals on a flower. If we were to do so, we would be surprised
to discover that the number of petals on a flower is one of the Fibonacci
numbers.
Lilies and iris
have 3 petals, buttercups have 5, some delphiniums have 8; corn marigolds have
13 petals; some asters have 21 whereas daisies can be found with 34, 55 or even
89 petals.
One petalled and two
petalled flowers are not common, yet we find white calla lily [Pic. No.7(a)] as
an one- petalled and euphorbia as a two- petalled flower [Pic. No.7(b)]. Three-
petalled [Pic. No.7(c)] are more common and we see it in flowers like lily,
iris. But lilies appear to have six petals. In fact, 3 are petals and 3 are
sepals. Sepals form the outer protection of the flowers when in bud. But almost
in all flowers difference between sepals and petals is clearly visible.
Pic.No.7a.
Euphorbia.
Pic. No. 7c

Trillium.
Very few plants show 4 petals or sepals, but some, such as fuchsia,
Gentian do. [PicNo.7(d)] Since 4 is not a Fibonacci number, then is it a break of natural law? We shall try to find an explanation later.
Pic. No. 7c

Very few plants show 4 petals or sepals, but some, such as fuchsia,
Gentian do. [PicNo.7(d)] Since 4 is not a Fibonacci number, then is it a break of natural law? We shall try to find an explanation later.
There are hundreds of species, both wild and cultivated, with
five petals. Such as buttercup, wild rose, larkspur, columbine, Adenium [Pic. No.7(e)]
pinks etc. The humble buttercup has been bred into a multi-petalled form
Pic. No.7d
Pic. No7e
Adenium.
Again, six is not a Fibonacci number yet there are six- petalled flowers, such as Blue – Eyed Grass [Pic. No.7(f)]. Eight- petalled flowers are not common as five- petalled, but there are quite a number of well-known species with eight. Such as delphiniums blood root and dahlia [Pic. No.7(g)]
Again, six is not a Fibonacci number yet there are six- petalled flowers, such as Blue – Eyed Grass [Pic. No.7(f)]. Eight- petalled flowers are not common as five- petalled, but there are quite a number of well-known species with eight. Such as delphiniums blood root and dahlia [Pic. No.7(g)]
Some of the
flowers with petals having the Fibonacci number 13 are ragwort, corn marigold,
cineraria, some daisies, black-eyed Susan.
The black-eyed
Susan belongs to the sunflower family as we see in the adjoining picture. [Pic. No.7(h)]
Pic.No.7f
Blue-eyed grass.
Pic.No.7f
Blue-eyed grass.
Pic. No7h
Black-eyed Susan.
Examples of flowers
with
21 petals- aster [Pic.
No.7(i)], chicory, Shasta daisy etc.
34 petals – plantain,
pyrethrum, some daises, chrysanthemum [Pic. No.7(j)]
55 and 89 petals – michaelmas daises, the asteraceae family
Pic. No7i
Twenty one and thirty four petals are quite common. The outer ring of ray
florets in the daisy family illustrate the Fibonacci sequence extremely well.
Daisies with 13, 21, 34, 55 or 89 petals are quite common.
In the pictures
we see the pyrethrum best known as chrysanthemum with 34 petals and michaelmas
daises, a close relative of asters with 55 and as much as 89 petals.
The Fibonacci
numbers pattern encountered herein occur so frequently that very often we term
the phenomenon as a “law of nature”.
But since 4 is
not a Fibonacci number, yet four- petalled flowers or four-leaf clover, a genus
of about 300 annual and perennial species in the pea family, are not rare in
the nature. Even large deviations from the Fibonacci patterns may also be
found. If it is at all disturbing to the modern botanists, it is not at all so
to the Fibonacci devotees, for whom the whole phenomenon, if not a law, is at
least a fascinating prevalent tendency!
The Fibonacci
numbers can also be found in the arrangement of seeds on flower heads. The
number of seeds and their spiral arrangements in the coneflowers and sunflowers
are worthy to mention for fitting well with Fibonacci numbers and the related
Golden Mean.
The coneflower is
a native North American sporting daisy like flower with raised centres. The
flower, plant and root of some types are used in herbal medicines.
Here in the
picture [Pic. No. 8a] of a
coneflower, we see that petals seem to form spirals running both to the left
and to the right. At the edge of the picture, if we count those spiralling to
the right as we go outwards, there are 55 spirals. A little further towards the
centre, the count is 34. Are these two numbers not the two consecutive Fibonacci
numbers? How many spirals we may expect at these places, if we go the other
way? We will find that the pair of numbers, curving left and curving right are
neighbours in the Fibonacci Series.
Pic. No. 8a
Sunflowers are
beautiful and iconic for the way their giant yellow heads against the back drop
of the blue sky. But have you ever stopped to look at the pattern of seeds held
within the centre of these special flowers? They are also a mathematical
marvel.
The seed heads of sunflowers optimize the packing of seeds by
arranging them in spirals of Fibonacci numbers. This patterning helps to pack
seeds uniformly with no crowding at the centre and no bald patches at the edges.
The Fibonacci
sequence fits so well for the sunflower because of its key characteristic –
growth. On a sunflower seed head, as an individual seed grows, the centre of
the seed head continues to add new seeds pushing those at the periphery
outwards. As a result, the seeds will always be packed uniformly and with
maximum compactness. [Pic. No. 8b]
Spirals of the Sunflower seed head.
In the spirals of the sunflower seed heads, there are two series of curves winding in opposite directions, starting at the centre and stretching out to the petals, with each seed sitting at a certain angle from the neighbouring seed to create the spiral.
In the spirals of the sunflower seed heads, there are two series of curves winding in opposite directions, starting at the centre and stretching out to the petals, with each seed sitting at a certain angle from the neighbouring seed to create the spiral.
On close
observations, it is found that in order to optimize in filling of the seeds in
the flower’s centre, it is necessary to choose a number that well approximated
by a fraction. This number is exactly the golden mean or golden ratio ( φ), an irrational number which has already been
mentioned. We may recall the value of this number
Φ =
1.6180339887 ---, the fractional part φ = 0. 6180339887 --- plays an important role
in filling the seeds.
The corresponding angle, the golden
angle is 137.5 degrees. This angle is chosen by the plants very precisely.
Otherwise variations of one tenth
of a degree
destroy completely the optimization. When the angle is exactly this golden
angle, two families of spirals, one in each direction are then visible.
Some fruits
like pineapple, banana, sharon fruit, apple and more, exhibit patterns
following Fibonacci sequence. When a banana or an apple is cut properly, it is
found that banana has 3 sections where as an apple has 5, both are Fibonacci
numbers.
Beautifully
grown pineapples with spirally arranged fruitlets follow a simple rule that
illustrates perfection in natural Fibonacci sequence.
On many
vegetables, we find the presence of Fibonacci numbers and golden means in their
formations, spirals, sections, seed heads etc.
Take for
example a cauliflower or a broccoli. If you count the number of florets in
spirals on a cauliflower, the number in one direction and in the other will be
Fibonacci numbers. Then to take a closer look at a single floret, break one off
near the base of the cauliflower. It is also a mini cauliflower with its own
little florets, all arranged in spirals around a centre. If possible, count
with patience, the spirals in both directions. Surprisingly counting them again
shows the Fibonacci numbers.
Philosophers,
scientists and artists believe that “Nature has designed the human body so that
its members are duly proportioned to the frame as a whole”. It is widely
believed that the human body follows the Golden Ratio.
An important relationship of golden section to design human body is that
there are : (i) 5 appendages to the torso, the trunk of the
human body, which are two arms, two legs and head.
(ii) 5 appendages on each of these,
the fingers and toes,
(iii) 5 openings on the face,
(iv) 5 sense organs for sight, sound, touch, taste and smell.
 Let us have a
close look at our hands. [Pic. No. – 9b]
Human hand has 5 fingers, each finger has 3 phalanx (bones of a finger or toe)
joints separated by two average sizes of falangelor, the lengths of bones of
fingers, are 2 cm, 3 cm, 5 cm. In continuation is a bone of the hand which has
an average length of 8 cm. Surprisingly, all these numbers belong to Fibonacci
sequence
Let us have a
close look at our hands. [Pic. No. – 9b]
Human hand has 5 fingers, each finger has 3 phalanx (bones of a finger or toe)
joints separated by two average sizes of falangelor, the lengths of bones of
fingers, are 2 cm, 3 cm, 5 cm. In continuation is a bone of the hand which has
an average length of 8 cm. Surprisingly, all these numbers belong to Fibonacci
sequence
Pic.No.9b
Moreover, each
section of our index finger, from the tip to the base of the wrist is longer
than the preceding one by about the Fibonacci ratio of 1.618, also fitting the
Fibonacci numbers 2, 3, 5 and 8. By this scale our fingernail is taken as a
unit.
Curiously enough
we have two hands, each with 5 digits and 8 fingers are each comprised of 3
sections. All are Fibonacci numbers!
Also our hand creates
a golden section in relation of our arm, as the ratio of our forearm to our
hand is also about 1.618, the Divine Proportions!
Even on our feet,
we may notice the presence of the golden section. Our foot has several
proportions based on phi lines, including
i) The middle of the
arch of the foot
ii) The widest part of
the foot.
iii) The base of the
toe line and big toe
iv) The top of the toe
line and base of the index toe.
The most
prominent, beautiful and important part of our human body is face [pic. No.9c ] considered
as the index of the mind.
pic.No.9c
Golden Ratio in human face.
Human face is
characterized in terms of aesthetic through several dimensions : The distance
between the eyes, distance between eyes and mouth, between eyes and nose, mouth
size. In terms of aesthetic in science that a girl appears more pleasant to our
eyes when these dimensions maintain the Fibonacci sequence better.
In this context,
I may ask, ‘Are you not amazed to look at the beauty of Mona Lisa, a half
portrait of a woman by the Italian artist Leonardo Da Vinci, which acclaimed as
the best known, most visited, the most written about, the most parodied work of
art in the world?’
The portrait
includes lot of Golden Rectangle, related to Golden Ratio. It is believed that
Leonardo as a mathematician tried to incorporate mathematics into art. This
painting seems to be made purposefully line up with golden rectangle.
But one thing is
to be kept in our mind that not every individual has body dimensions in exact
proportion but averaged across the population tend towards phi and the phi
proportions are perceived as being the most natural or beautiful.
We have already
seen the spiral arrangements in leaves, arrangements of florets in flowers and
on fruits. But have you ever looked at an interactive weather map depicting
hurricane activity? If you have observed, you will be convinced to believe that
a hurricane takes a spiral shape and most probably you will draw an analogy
with the shape of a seashell or a winding stair case. Yes, they have the same
shape and what you are observing is called Fibonacci spiral. This spiral shows
up in many areas of nature, art, architecture, astronomy, oceanography and many
other places.
You will be surprised
to know that the shape of this spiral obeys some definite mathematical rules
and the answer of this puzzle lies in golden rectangle.
All of us are
familiar with this geometrical figure of a rectangle. But do you have a
rectangle size that is your favourite? Is it an odd question? No, not always,
for there is a certain type that is found to be aesthetically pleasing to the eye. That is the golden rectangle.
i)
Construct a simple square of your choice.
ii) Draw a line from the midpoint of one
side of the square to an opposite corner.
iii) Taking that line as the radius, draw an
arc that defines the height of the rectangle.
iv) Complete the rectangle.
This will be a golden
rectangle.]
Pic.
No. 10a
A Golden Rectangle.
Now the question is,
how is the Fibonacci spiral related to the golden rectangle? The answer is :
the golden rectangle has a unique property that when a square is removed, a
smaller rectangle of the same shape, and of course a golden rectangle, remains.
Thus a smaller square can be removed and so on and on, resulting with a spiral
pattern. This is exactly the Fibonacci spiral. It will be clear from the
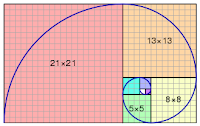
adjoining picture. [Pic. No. 10b]
Pic.No 10b.
Pic.No 10b.
If we look closely
at the animal world around us, we will find not only beauties in them but also
the presence of the golden section or Divine Proportions in their bodies.
Here are some examples which will
illustrate this.
Dolphin
: The eye, fins and tail all fall at golden sections of the length of the
dolphin’s body. The dimensions of the dorsal fin are golden sections (yellow
and green). The thickness of the dolphin’s tail section corresponds to same
golden section of the line from head to tail. [Pic. No. – 11a]
Pic.No1 11a.
Pic.No1 11a.
Golden Ratio on Dolphin.
.
.
Moth : The
eye-like markings of this moth fall at golden sections of the lines that mark
its width and length. [Pic. No. 11b]
Angel fish : Every
key body feature of the angel fish falls at golden sections of its width and
length, such as nose, tail sections and centres of the fins firstly and indents
of the dorsal and tail find as well as the top of the body secondly. It is also
observed around the eye. [Pic. No. 11c]
Pic.No11c.
Pic.No11c.
Penguin : The
eyes, beak, wing and key body markings of the penguin all fall at golden
sections of its height. [Pic. No. 11d]
Pic.No11d.
Pic.No11d.
Golden Ratio on Penguin.
Tiger : All key
facial features of the tiger fall at golden sections of the lines defining the
length and width of its face. [Pic. No.
11e]
Golden Ratio on Tiger face.
Ant : The body
sections of an ant are defined by the golden sections of its length, its leg
sections are also golden sections of its length. [Pic. No. 11f]
Golden Ratio on Ant.
Sea-shell : The
spiral growth of Sea-shells provide a simple but beautiful example. [Pic. No. 11g]
Golden Ratio on Seashell.
Luca Pacioli, a contemporary of the
legendary genius Leonardo Da Vinci once said, ‘Without mathematics there is no
art.’
We have already found the presence
of golden section in the design and beauty of nature. It can also be used to
achieve beauty, balance and harmony in art and design. It’s a tool not a rule,
for composition. But learning how to use it can be great art on laying out a
painting on a canvas.
For those with greater
understanding yet, the golden ratio can be used in more elegant ways to create
aesthetics and visual harmony, in any branch of the design arts as it is found
to be used by the greatest artists world has known.
But oddly enough some staunch
critics may be found who say that the golden ratio cannot be found in art at
all, for it has an infinite number of digits ( we may recall that (Φ
=
1.61803398875 ---- ). By a similar reasoning, a pi (π) the ratio of the
circumference of a circle to its diameter, does too (π =3.14159 ---), so there
can be no circle in the real world. Whatever those critics may say, for the
rest of us, practical applications of mathematical concepts are a simple and
everyday occurrence in arts, engineering and applied sciences.
Now we may find below the presence of golden rectangle and golden ratio
in some unforgettable paintings of some legendary artists, the world has ever
seen and also in some wonders of architectures strewn around the world.
Mona Lisa: By Leonardo Da Vinci (1452 – 1519)
This picture includes lots of
Golden Rectangles. In this figure, we can draw a rectangle whose base extends
from the woman’s right wrist to her left elbow and extend the rectangle
vertically until it reaches the very top of her head, then we will have golden
rectangle. [Pi c. No. 12a]
Pic.No12a.
Golden Ratio in Mona Lisa.
Also if we draw squares inside this golden rectangle, we will discover
that the edges of these new squares come to all the important focal points of
the woman : her chin, eye, nose and the upturned corner of her mysterious
mouth.
Holy Family: By Michelangelo (1475
– 1564)
We can notice that this picture is
positioned to the principal figures in alignment with a Pentagram or Golden Star.
[Pic. No.12b]
Pic.No12b.
Pic.No12b.
Holy Family in a Golden star.
Pentagram, a star
shaped symbol enclosed in a circle has a deeper meaning. Of the five points,
one always pointing upward is representative of spirit and the other four
points represent the elements of earth, air, fire and water. All these things
are parts of life of each of us.
Moreover, the
number 5 is always been regarded as mystical and magical yet essentially human;
for we have many aspects of our body consisting of 5 parts, such as fingers,
toes, senses etc.
A fresco in Vatican Palace: By Raphael
(1483 – 1520)
The picture is from the Stanza Della
(The school of Athens) Segnatura, The room of the Segnatura is decorated by
Raphael’s most famous frescoes, besides being the first work executed by the
great artist in Vatican.
Raphael’s ‘School
of Athens’ provides another wonderful example of the application of the golden
ratio in composition. A small golden rectangle at the front and centre of the
painting signals the artist’s intent in the use of this proportion. It gives
the paintings a wonderful visual harmony. [Pic.
No.- 12c]
Pic.No12c.
A fresco in a Golden Rectangle.
Self – Portrait : By Rembrandt (1606 – 1669)
We can draw three straight lines in to this picture. Then,
the image of the feature is included into a triangle. Moreover, if a
perpendicular line would be dropped from the apex of the triangle to the base,
the line would cut the base in golden ratio. [Pic. No.12d]
Pic.No12d.
Self -Portrait by Rembrandt.
Pic.No12d.
Self -Portrait by Rembrandt.
The Sacrament of the Last Supper:
By Salvador Dali (1904 -1989)
This picture is painted inside a
golden rectangle. Also, we can find part of an enormous dodecahedron above the
table. Since the polyhedron consists of 12 regular pentagons, it is closely
connected to the golden section. [Pic.
No.12e]
Pic. No.12e
Bathers: By Georges Seurat
(1859-1891)
Seurat attached most of Canvas by the golden section. This
picture has several golden subdivisions. [Pic.
No.- 12f]
Bathers.
The Golden Stairs : By
Edward Burne Jones (1833 – 1898) [Pic.
No. 12 g]
The Golden Stairs.
The artist meticulously planned the
minute of details using golden section. If we cast a close look at the
painting, we may notice that golden section appear in the stairs and the ring
of the trumpet carried by the fourth woman from the top. The lengths of the
gowns from sash below the breast to the bottom helm hits the phi point at their
knees. The width of the interior door at the back of the top of the stairs is a
golden section of the width of the top of the opening of the sky light. So,
there are a lot of things of the golden ratio in the picture!
The above
examples are only a very few. There are a pretty large number of applications
of this golden ratio in paintings of many legendary artists.
We may also be
surprised to find the traces of this golden ratio in construction marvels of
many famous monuments, wonders of the world, temples, chapels, basilicas,
places of worship, even in some modern buildings and complexes, all over the
world.
We may cite some
examples of these marvels.
The great pyramid
of Giza in Egypt is the most substantial ancient structure in the world and
most mysterious also. The three pyramids on the Giza plateau are funerary
structures of three Egyptian kings of the fourth dynasty during 2575 to 2465
B.C.
The great pyramid
was originally 481 feet 5 inches tall and measured 755 feet along its sides,
covering an area of 13 acres, constructed from approximately 2.5 million lime
stone blocks weighing on an average of 2.6 tons each.
The ancient
Egyptians were first to use mathematics in art. It seems almost certain that
they ascribed magical proportion of the golden section and used in the design
of their great pyramids.
If we take a
cross section of the Great pyramid, we get a right-angled triangle, the so
called Egyptian triangle. The ratio of the slant height of the pyramid, here
the hypotenuse of the triangle, to the distance from the ground centre, which
is half the dimension, is 1.61804 and surprisingly it matches with the value of
phi, the golden ratio.[Pic. No.13a]
The Great Pyramid of Giza.
The Egyptians thought the golden ratio is sacred. Therefore it was important in their religion. They used the golden ratio in building temples and places for the dead. They were aware that they were using the golden ratio but they called it ‘Sacred ratio’.
The Egyptians thought the golden ratio is sacred. Therefore it was important in their religion. They used the golden ratio in building temples and places for the dead. They were aware that they were using the golden ratio but they called it ‘Sacred ratio’.
We have evidences
that Greeks were also acquainted with golden ratio from ancient times. AS an
example, they applied it in the architecture of Parthenon,Chief temple [Pic. No.13b] of the Greek goddess
Athena, the virgin, on the hills of Acropolis at Athens. It was built in the
mid. 5th century BC. The name Parthenon refers to the cult of
Athena Parthenon. Work began in 447 BC and it was completed by 438 BC. The
same year a great gold and ivory statue of Athena, made by Phidias for the
interior, was dedicated. Work on the exterior decoration of the building
continued until 432 BC. One interesting aspect is that, all temples in Greece
were designed to be seen only from the outside. The viewers never entered a
temple and could only glimpse the interior statues through the open doors. The
Greek sculpture Phidias sculpted many things including the bands of sculpture
that run above the column of the Parthenon. The Parthenon was perhaps the best
example of mathematical approach to art. Once its ruined triangular pediment is
restored, the ancient temple site almost perfectly in to a golden rectangle.
Pic.No13b.
Pic.No13b.
Now let us explore a monument of immeasurable beauty, the Taj
Mahal, one of the Seven Wonders of the World and now a UNESCO world heritage
site, standing majestically on the bank of the River Yamuna flowing by the
historically famous city of Agra in India. The visceral charisma it emanates is
closely related to golden section. [Pic.
No.-13c]
Pic. No.-13c
Golden Ratio in Taj Mahal.
Pic.No.5 Leaf arrangements in Sunflower plant
Dr.Ron Knott: ( http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/fibnat.html
Attribution:
Pic.No 9a,b,c---Golden Ratio in human body,hand and face respectively
International Journal of Arts 2011 (https://pdfs.semanticscholar.org/1f56/48a45169c011c82a23273f30cc297850484a.pdf )
Image credit:Pic.No 11a,b,c,d,e,f,g---Golden Ratio on Dolphin, Moth,Angel fish,Penguin,Tiger face,Ant,Shell respectively: J.W. Wilson.
( http://jwilson.coe.uga.edu/EMT668/EMAT6680.F99/Hekimoglu/emat6700/golden%20ratio/animalgold.html )
Pic.No 12 a,b,c,d,e,f,---Golden Ratio in Mona Lisa,Holy Family,Fresco in Vatican Palace,self portrait by Rembrandt,Last Supper,Bathers Pic.No 13a Great Pyramid in Giza,13b Parthenon: Samuel Obara (ref.J. Wilson )
( http://jwilson.coe.uga.edu/emt668/EMAT6680.2000/Obara/Emat6690/Golden%20Ratio /golden.html)
Pic.No13c. Goloden Ratio shown on Taj Mahal
Image credit: Wikimedia Cosmos (https://en.wikipedia.org/wiki/Taj_Mahal )
Pic.No13d.Golden Ratio shown on Eiffel Tower
Image credit:Wikimedia Cosmos
( https://en.wikipedia.org/wiki/Eiffel_Tower#/media/File:Tour_Eiffel_Wikimedia_Commons_(cropped).jpg )
Golden Ratio in Taj Mahal.
The Taj Mahal is
synonymous to love and romance and considered to be an “epitome of love”. The
name ‘Taj Mahal’ was derived from the name of the Mughal emperor Shah Jahan’s
wife, Mumtaz Mahal and means “Crown Palace”.
The purity of the
white marble, the exquisite ornamentation, precious gemstones and its
picturesque location, all make a visit to the Taj Mahal gain a place amongst
the most sought after tours in the world.
Here one thing is
to be kept in mind that it is not just an outstanding beautiful building
monument, it is the love behind which has given a life to it.
But why are we so
amazed with the beauty of Taj Mahal? For at the brink of dawn when the first
rays of the sun hits the dome of this epic monument, it radiates like a
heavenly abode, cloaked in bright golden and at dusk, basking in the glory of
moon, it shines like a perfectly carved diamond, leaving the viewers awe struck
by its sense of grandeur.
Taj Mahal was built in 22 years (1631 - 1653).
20000 workers laboured and 32 crores of rupees spent, which may amount now to
the budget of our one of the five-year plans of several lakh crores rupees.
The architectural
of the Taj Mahal mausoleum amazes every visitor for more than three and a half
hundred years. The complex consists of:
The mausoleum ensembles
with four minarets stand on the quadrant podium approximately 120 x 120 m.
Two buildings
aside of the ensemble standing symmetrical to it, the mosque and Jamaat Khana,
meaning meeting place.
And the garden is
approximately 320 x 320 m.
Huge scale of the
whole complex is only an accompaniment to the refined architecture of the tomb
ensemble.
Decoded
geometrical structure of the Taj Mahal mausoleum’s architectural composition
reveals that the idea of the Taj Mahal is rationally and intently based on golden
section, as so as all non-Golden regularities are hierarchically dependent to
the Golden ones. Main entrance door frame rectangle is accurately golden
rectangle. Geometry of the arc inside it is as well built after golden
regularities.
Geometry of the
garden plan, places and sizes of the buildings are clear and nothing but
rectangle. But it is hard even to compare the simplicity of the master plan
with high complexity of the proportional hierarchy of the tomb ensemble’s
composition.
Another example of
application of golden ratio in architecture, is the Eiffel Tower, an
engineering marvel at Champ-de-Mars, a public large green space by the side of
the river Seine, located in central Paris, France. [Pic. No.- 13d]
Pic. No. 13d
Golden Ratio in Eiffel Tower.
It was built as
an entrance to “Exposition Universelle” – the World’s Fair, hosted in 1889 to
mark 100 year anniversary of the French Revolution. The name ‘Eifel Tower’
derived from the name of its builder Alexandre Gustave Eiffel, an acclaimed
bridge builder, architect and metal expert.
Of the plans
submitted by more than 100 artists to build the monument for the fair,
Alexandre Gustave Eiffel’s consulting and construction firm was finally
entrusted with the job.
The final design
called for more than 18000 pieces of a special type of wrought iron used in
constructions and 2.5 million rivets assembling the framework of the iconic
lattice tower, which at the time of inauguration in March 1889 stood nearly
1000 ft. high and the tallest structure of the world at that time. Later in
1957, an antenna was added that increased the structure’s height by 65 feet.
Initially, only the Eiffel tower’s second platform was open to the public,
latter all three levels, two of which now feature restaurants, would be
reachable by stairway or one of the eight elevators.
Millions of
visitors during and after the World’s Fair marveled at Paris’ newly erected
architectural wonder. But many Parisians were of different opinion. They
thought it was structurally unsound and even some considered it an eyesore. For
example, the noted novelist Guy de Maupassant allegedly hated the tower so much
that he often ate lunch in the restaurant at its base choosing a vantage point
to sit, so that he could completely avoid glimpsing its looming silhouette.
The Eiffel Tower
was originally intended as a temporary exhibit and so it was almost dismantled
and scrapped in 1909. But it was realized by the civic authority later that
this structure may be used to set up a radiotelegraph station on it. So it was
restored. During World War – I, this tower intercepted enemy’s many radio
communications and helped a lot in army operations. During World War – II Hitler
ordered to destroy it but that order was never carried out and this iconic
tower was saved for the second time.
Since then much
water had flown through the river Seine, Eiffel Tower has been the site of
numerous high profile stunts, ceremonial events and even scientific
experiments. Now one of the most recognizable structures in the world, the
Eiffel Tower underwent a major face-list in 1986 and is repainted in every seven
years. It welcomes more visitors than any other monument in our globe – an
estimated average of 7 million people per year The Eiffel Tower also inspired
more than 30 replicas and similar structures in various cities around the
world.
But keeping aside
all praises, criticisms and apathies concerning the Eiffel Tower, we are curious
to know whether the golden ratio has any role to play in the construction of
this structure. Surprisingly yes! The taper of the tower at major subdivisions
– the first stage, second stage, the intermediate platform and the third stage
or top appears to follow multiples of golden ratio.
The ratio of the
width of the base to the width of tower of the first stage is 1.62 (fairly
equals to the value of the golden ratio, phi). At the second stage, it is 2 x
1.62, at the intermediate platform, 4 x 1.62 and at the top about 8 x 1.62.
There are much
more examples of application of golden ratio in architecture. Some of them are
worthy to be mentioned as:
The famous,
historic Notre Dame Cathedral in Paris, the United Nation’s Secretariat
building in New York, the CN Tower in Toronto the tallest and free standing
structure in the world.
It is found
surprisingly that the number of atheists – namely, the persons, who disbelieve
in the existence of a creator like God and hence belong to no religion, is so
insignificant that may be ignored altogether. Almost all people of the world
population belong to one or other religion. Again there lies a creator, as they
believe at the core of every religion who is behind this beautiful, fantastic
yet perilous universe. Many scientist of world fame are no exceptions.
Some specific
secret rules and surprising orders those exhibited in a multitude of shapes and
patterns whose relationship can only be the result of an omnipotent, good and
all-wise God of scripture. This secret is now attributed to the role of Divine
Proportion, existing in the smallest to the largest parts, in living and also
in non-living things --- reveals the awesome handiwork of God and His interest
in beauty, function and order.
We find things
of various shapes around us in the nature of which spiral shape is most common
and familiar to us. It is visible as diverse as shells, hurricanes, spiral
seeds, the cochlea of the human ear, ram’s horn, the curl of an elephant tusk,
sea-horse tail, growing fern leaves, DNA molecules, waves breaking on the
beach, tornado, galaxies, distribution of planets in the solar system, the tail
of a comet as it winds around the sun, whirlpools, seeds patterns of many
flowers and so many. These spirals follow a precise mathematical pattern.
We have already
seen that there are many many evidences of the presence of golden ratio in the
nature around us as well as in arts, architecture etc. But if we think on a
larger perspective, we find that this divine ratio has a great role to play on
the functioning of our universe also.
Albert Einstein
(1879 – 1955), perhaps the greatest scientist of the twentieth century, has
proved beyond doubt that the vast space of this universe in which lie about 170
billion galaxies containing two to four billion stars, with their satellites,
six on an average including our solar system – our earth and of course we ourselves,
the vast inter stellar space etc. behaves like a sheet of rubber and hence bend
with the weight of the heavenly bodies lying on it.
His epoch making
discovery that time is interwoven with this space and time to be regarded as
the fourth dimension. The other three, as we know, are length, breadth and
height of a material body. The space and time together termed as “Space Time”.
Modern researchers claim that this universe is governed by the divine ratio,
the space-time itself is defined by this mathematical constant ratio of 1.618,
the golden ratio.
On the
perspective of the “Multiverse” theory (many universes like that of ours), they
suggested that our universe to have this ratio that allowed it to form as is
observed now.
But can all the
natural phenomena be bounded by the Fibonacci numbers only? The answer would be
an emphatic ‘No’. The whole of the universe is definitely guided by some
mathematical order but little of them are within our reach. Up till now, we are
able to unravel out only a bit of the mysteries of the nature, which is nothing
but a tip of an ice berg. The most are shrouded in darkness. There are 100s of
what, why, when, where and how.
So, if you find
the numbers 1, 2, 3 and 5 occurring some where it does not always mean the
Fibonacci numbers although they could be.
There are many
examples where Fibonacci numbers do not appear in plants. For example:
a 4 leaved clover, a Fuchsia has
4 petals and 4 sepals, some white sweet peppers have 4 chambers.
There are many flowers with six petals, such as crocus,
narcissus, amaryllis, blue-eyed grass. [
Succulents with clear arrangements
are of 4 spirals in one direction and 7 in the other or 11 and 18 spirals.
Many cacti do not show Fibonacci
numbers.
So, it is clear that not all
plants show Fibonacci number but another series of numbers, called Lucas
numbers. But what is it?
The French mathematician Edward Lucas (1842 – 1891), who gave the series
0, 1, 1, 2, 3, 5, 8, - - - , the name Fibonacci numbers found a similar series
occurs often when he was investigating
Fibonacci numbers patterns, which is as 2, 1, 3, 4, 7, 11, 18, 29 - - -
The Lucas numbers have lots of
properties similar to those of Fibonacci numbers. In fact, for every series
formed by adding the latest two values to get the next, and no matter what two
positive numbers we start with, we will always end up having terms whose ratio
is 1.6189339 - - -- our well known golden ratio!
In fact, no matter what two
numbers we begin with, the ratio and two successive numbers in all these
Fibonacci type sequences always approach a spiral value the golden mean and
thus seems to be the secret behind the series.
Hence it is amply clear that
some plants do not manifest Fibonacci numbers but sometimes Lucas numbers or
even more anomalous sequence 5, 1,4, 5, 7 - - - - or 5, 2, 7, 9, 16 - - -
So, we should admit that phyllotaxis is really not a universal law but
fascinatingly a prevalent tendency.
[To continue]
Reference Internet: Images are downloaded from Public Domain (except otherwise stated)Pic.No.5 Leaf arrangements in Sunflower plant
Dr.Ron Knott: ( http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/fibnat.html
Attribution:
Pic.No 9a,b,c---Golden Ratio in human body,hand and face respectively
International Journal of Arts 2011 (https://pdfs.semanticscholar.org/1f56/48a45169c011c82a23273f30cc297850484a.pdf )
Image credit:Pic.No 11a,b,c,d,e,f,g---Golden Ratio on Dolphin, Moth,Angel fish,Penguin,Tiger face,Ant,Shell respectively: J.W. Wilson.
( http://jwilson.coe.uga.edu/EMT668/EMAT6680.F99/Hekimoglu/emat6700/golden%20ratio/animalgold.html )
Pic.No 12 a,b,c,d,e,f,---Golden Ratio in Mona Lisa,Holy Family,Fresco in Vatican Palace,self portrait by Rembrandt,Last Supper,Bathers Pic.No 13a Great Pyramid in Giza,13b Parthenon: Samuel Obara (ref.J. Wilson )
( http://jwilson.coe.uga.edu/emt668/EMAT6680.2000/Obara/Emat6690/Golden%20Ratio /golden.html)
Pic.No13c. Goloden Ratio shown on Taj Mahal
Image credit: Wikimedia Cosmos (https://en.wikipedia.org/wiki/Taj_Mahal )
Pic.No13d.Golden Ratio shown on Eiffel Tower
Image credit:Wikimedia Cosmos
( https://en.wikipedia.org/wiki/Eiffel_Tower#/media/File:Tour_Eiffel_Wikimedia_Commons_(cropped).jpg )
Golden Ratio in Taj Mahal.
The Taj Mahal is synonymous to love and romance and considered to be an “epitome of love”. The name ‘Taj Mahal’ was derived from the name of the Mughal emperor Shah Jahan’s wife, Mumtaz Mahal and means “Crown Palace”.
The Taj Mahal is synonymous to love and romance and considered to be an “epitome of love”. The name ‘Taj Mahal’ was derived from the name of the Mughal emperor Shah Jahan’s wife, Mumtaz Mahal and means “Crown Palace”.
The purity of the
white marble, the exquisite ornamentation, precious gemstones and its
picturesque location, all make a visit to the Taj Mahal gain a place amongst
the most sought after tours in the world.
Here one thing is
to be kept in mind that it is not just an outstanding beautiful building
monument, it is the love behind which has given a life to it.
But why are we so
amazed with the beauty of Taj Mahal? For at the brink of dawn when the first
rays of the sun hits the dome of this epic monument, it radiates like a
heavenly abode, cloaked in bright golden and at dusk, basking in the glory of
moon, it shines like a perfectly carved diamond, leaving the viewers awe struck
by its sense of grandeur.
Taj Mahal was built in 22 years (1631 - 1653).
20000 workers laboured and 32 crores of rupees spent, which may amount now to
the budget of our one of the five-year plans of several lakh crores rupees.
The architectural
of the Taj Mahal mausoleum amazes every visitor for more than three and a half
hundred years. The complex consists of:
The mausoleum ensembles
with four minarets stand on the quadrant podium approximately 120 x 120 m.
Two buildings
aside of the ensemble standing symmetrical to it, the mosque and Jamaat Khana,
meaning meeting place.
And the garden is
approximately 320 x 320 m.
Huge scale of the
whole complex is only an accompaniment to the refined architecture of the tomb
ensemble.
Decoded
geometrical structure of the Taj Mahal mausoleum’s architectural composition
reveals that the idea of the Taj Mahal is rationally and intently based on golden
section, as so as all non-Golden regularities are hierarchically dependent to
the Golden ones. Main entrance door frame rectangle is accurately golden
rectangle. Geometry of the arc inside it is as well built after golden
regularities.
Geometry of the
garden plan, places and sizes of the buildings are clear and nothing but
rectangle. But it is hard even to compare the simplicity of the master plan
with high complexity of the proportional hierarchy of the tomb ensemble’s
composition.
Another example of
application of golden ratio in architecture, is the Eiffel Tower, an
engineering marvel at Champ-de-Mars, a public large green space by the side of
the river Seine, located in central Paris, France. [Pic. No.- 13d]
Golden Ratio in Eiffel Tower.
It was built as an entrance to “Exposition Universelle” – the World’s Fair, hosted in 1889 to
mark 100 year anniversary of the French Revolution. The name ‘Eifel Tower’ derived from the name of its builder Alexandre Gustave Eiffel, an acclaimed bridge builder, architect and metal expert.
It was built as an entrance to “Exposition Universelle” – the World’s Fair, hosted in 1889 to
mark 100 year anniversary of the French Revolution. The name ‘Eifel Tower’ derived from the name of its builder Alexandre Gustave Eiffel, an acclaimed bridge builder, architect and metal expert.
Of the plans
submitted by more than 100 artists to build the monument for the fair,
Alexandre Gustave Eiffel’s consulting and construction firm was finally
entrusted with the job.
The final design
called for more than 18000 pieces of a special type of wrought iron used in
constructions and 2.5 million rivets assembling the framework of the iconic
lattice tower, which at the time of inauguration in March 1889 stood nearly
1000 ft. high and the tallest structure of the world at that time. Later in
1957, an antenna was added that increased the structure’s height by 65 feet.
Initially, only the Eiffel tower’s second platform was open to the public,
latter all three levels, two of which now feature restaurants, would be
reachable by stairway or one of the eight elevators.
Millions of
visitors during and after the World’s Fair marveled at Paris’ newly erected
architectural wonder. But many Parisians were of different opinion. They
thought it was structurally unsound and even some considered it an eyesore. For
example, the noted novelist Guy de Maupassant allegedly hated the tower so much
that he often ate lunch in the restaurant at its base choosing a vantage point
to sit, so that he could completely avoid glimpsing its looming silhouette.
The Eifel Tower
was originally intended as a temporary exhibit and so it was almost dismantled
and scrapped in 1909. But it was realized by the civic authority later that
this structure may be used to set up a radiotelegraph station on it. So it was
restored. During World War – I, this tower intercepted enemy’s many radio
communications and helped a lot in army operations. During World War – II Hitler
ordered to destroy it but that order was never carried out and this iconic
tower was saved for the second time.
Since then much
water had flown through the river Seine, Eifel Tower has been the site of
numerous high profile stunts, ceremonial events and even scientific
experiments. Now one of the most recognizable structures in the world, the
Eifel Tower underwent a major face-list in 1986 and is repainted in every seven
years. It welcomes more visitors than any other monument in our globe – an
estimated average of 7 million people per year The Eifel Tower also inspired
more than 30 replicas and similar structures in various cities around the
world.
But keeping aside
all praises, criticisms and apathies concerning the Eifel Tower, we are curious
to know whether the golden ratio has any role to play in the construction of
this structure. Surprisingly yes! The taper of the tower at major subdivisions
– the first stage, second stage, the intermediate platform and the third stage
or top appears to follow multiples of golden ratio.
The ratio of the
width of the base to the width of tower of the first stage is 1.62 (fairly
equals to the value of the golden ratio, phi). At the second stage, it is 2 x
1.62, at the intermediate platform, 4 x 1.62 and at the top about 8 x 1.62.
There are much
more examples of application of golden ratio in architecture. Some of them are
worthy to be mentioned as:
The famous,
historic Notre Dame Cathedral in Paris, the United Nation’s Secretariat
building in New York, the CN Tower in Toronto the tallest and free standing
structure in the world.
It is found
surprisingly that the number of atheists – namely, the persons, who disbelieve
in the existence of a creator like God and hence belong to no religion, is so
insignificant that may be ignored altogether. Almost all people of the world
population belong to one or other religion. Again there lies a creator, as they
believe at the core of every religion who is behind this beautiful, fantastic
yet perilous universe. Many scientist of world fame are no exceptions.
Some specific
secret rules and surprising orders those exhibited in a multitude of shapes and
patterns whose relationship can only be the result of an omnipotent, good and
all-wise God of scripture. This secret is now attributed to the role of Divine
Proportion, existing in the smallest to the largest parts, in living and also
in non-living things --- reveals the awesome handiwork of God and His interest
in beauty, function and order.
We find things
of various shapes around us in the nature of which spiral shape is most common
and familiar to us. It is visible as diverse as shells, hurricanes, spiral
seeds, the cochlea of the human ear, ram’s horn, the curl of an elephant tusk,
sea-horse tail, growing fern leaves, DNA molecules, waves breaking on the
beach, tornado, galaxies, distribution of planets in the solar system, the tail
of a comet as it winds around the sun, whirlpools, seeds patterns of many
flowers and so many. These spirals follow a precise mathematical pattern.
We have already
seen that there are many many evidences of the presence of golden ratio in the
nature around us as well as in arts, architecture etc. But if we think on a
larger perspective, we find that this divine ratio has a great role to play on
the functioning of our universe also.
Albert Einstein
(1879 – 1955), perhaps the greatest scientist of the twentieth century, has
proved beyond doubt that the vast space of this universe in which lie about 170
billion galaxies containing two to four billion stars, with their satellites,
six on an average including our solar system – our earth and of course we ourselves,
the vast inter stellar space etc. behaves like a sheet of rubber and hence bend
with the weight of the heavenly bodies lying on it.
His epoch making
discovery that time is interwoven with this space and time to be regarded as
the fourth dimension. The other three, as we know, are length, breadth and
height of a material body. The space and time together termed as “Space Time”.
Modern researchers claim that this universe is governed by the divine ratio,
the space-time itself is defined by this mathematical constant ratio of 1.618,
the golden ratio.
On the
perspective of the “Multiverse” theory (many universes like that of ours), they
suggested that our universe to have this ratio that allowed it to form as is
observed now.
But can all the
natural phenomena be bounded by the Fibonacci numbers only? The answer would be
an emphatic ‘No’. The whole of the universe is definitely guided by some
mathematical order but little of them are within our reach. Up till now, we are
able to unravel out only a bit of the mysteries of the nature, which is nothing
but a tip of an ice berg. The most are shrouded in darkness. There are 100s of
what, why, when, where and how.
So, if you find
the numbers 1, 2, 3 and 5 occurring some where it does not always mean the
Fibonacci numbers although they could be.
There are many
examples where Fibonacci numbers do not appear in plants. For example:
a 4 leaved clover, a Fuchsia has
4 petals and 4 sepals, some white sweet peppers have 4 chambers. [Pic.
No.-7(d)]
There are many flowers with six petals, such as crocus,
narcissus, amaryllis, blue-eyed grass. [Pic. No.-7(f)]
Succulents with clear arrangements
are of 4 spirals in one direction and 7 in the other or 11 and 18 spirals.
Many cacti do not show Fibonacci
numbers.
So, it is clear that not all
plants show Fibonacci number but another series of numbers, called Lucas
numbers. But what is it?
The French mathematician Edward Lucas (1842 – 1891), who gave the series
0, 1, 1, 2, 3, 5, 8, - - - , the name Fibonacci numbers found a similar series
occurs often when he was investigating
Fibonacci numbers patterns, which is as 2, 1, 3, 4, 7, 11, 18, 29 - - -
The Lucas numbers have lots of
properties similar to those of Fibonacci numbers. In fact, for every series
formed by adding the latest two values to get the next, and no matter what two
positive numbers we start with, we will always end up having terms whose ratio
is 1.6189339 - - -- our well known golden ratio!
In fact, no matter what two
numbers we begin with, the ratio and two successive numbers in all these
Fibonacci type sequences always approach a spiral value the golden mean and
thus seems to be the secret behind the series.
Hence it is amply clear that
some plants do not manifest Fibonacci numbers but sometimes Lucas numbers or
even more anomalous sequence 5, 1,4, 5, 7 - - - - or 5, 2, 7, 9, 16 - - -
So, we should admit that phyllotaxis is really not a universal law but
fascinatingly a prevalent tendency.












































No comments:
Post a Comment